Syntactic Analysis and Abstract Syntax Trees

I decided to write this post because I am studying for my final exam in compiler design and I would like to go over some topics I find interesting.

Syntactic Analyzer 🔗

Syntactic analysis is the problem of deciding whether an input string can be recognized by the provided grammar. This can be done by constructing a derivation tree for the input string – finding production rules to be applied in order to generate the input string. In the case of compilers, we’re trying to decide whether the provided symbols form a valid program in the programming language. Since the problem of syntactic analysis is hard to solve for context-free grammars in general, programming language designers turn to subsets of such grammars, e.g. LL(k), LR(k), LALR, and SLR grammars, which are less powerful than context-free grammars, but more powerful than regular grammars. For example, in LL(1) grammars, we’re allowed to peek one symbol ahead when analyzing the input in order to decide what production rule to choose.

Syntactic analysis is performed by a parser (syntactic analyzer), which is the second stage in the compiler pipeline. It fetches a list of lexems from the lexical analyzer (lexer), which reads the input program, builds a tree structure from the linear stream, and passes it to the semantic analyzer. In most compilers, parser is the component which leads the cooperation between the lexical, syntactic, and semantic analyzer. It is important to note that entire input may not be analyzed at once. Parser can work on just a portion of the input program and pass it to the semantic analyzer.

The parser has 2 main objectives: it verifies the syntactic soundness of the input text according to the provided grammar and passes semantically important information to the semantic analyzer. It can also choose the direction of parsing: it can either work in top-to-bottom manner, starting from the starting non-terminal and expanding it until all the input symbols matched or the other way around, gradually reading input and reducing the symbols into non-terminals until the starting non-terminal is reached.

Syntax Verification 🔗

As noted above, parsers verify the input text by performing syntactic analysis. If the parser can build (not necessarily explicitely) the derivation tree for the input program, the input is deemed valid. This can be done in several ways: by recursive descent parsing (if the grammar describing the language is an LL(k) grammar) or other parsers, such as LALR parser or SLR parsers and feeding the input to the parser.

Recursive Descent Parsing 🔗

This method is probably the most intuitive to grasp and to construct by both compiler programmers and compiler-compilers and is done when working with LL(k) languages. It is done by building recursive finite-state machines, which is just a set of deterministic finite-state automata recursivelly calling each other. Each automaton has two types of actions: it either reads the symbol from the input, if it’s a terminal symbol, or calls another automaton associated with the given non-terminal. Only limitation is that with a given non-terminal, at most one automaton must be associated.

Let G be a context-free grammar with terminals Σ = {+, *, id, (, )} and non-terminals N = {E, E', T, T', F} and the following production rules P:

P = {
    E := E + T | T
    T := T * F | F
    F := id    | (E)
}

Using production rules P does not make the grammar G LL(k). Instead, we have to (equivalently) re-write the rules accordingly:

P = {
    E  := TE'
    E' := +TE' | ε
    T  := FT'
    T' := *FT' | ε
    F  := id   | (E)
}

Now we can simply create an automaton associated with each non-terminal as follows:

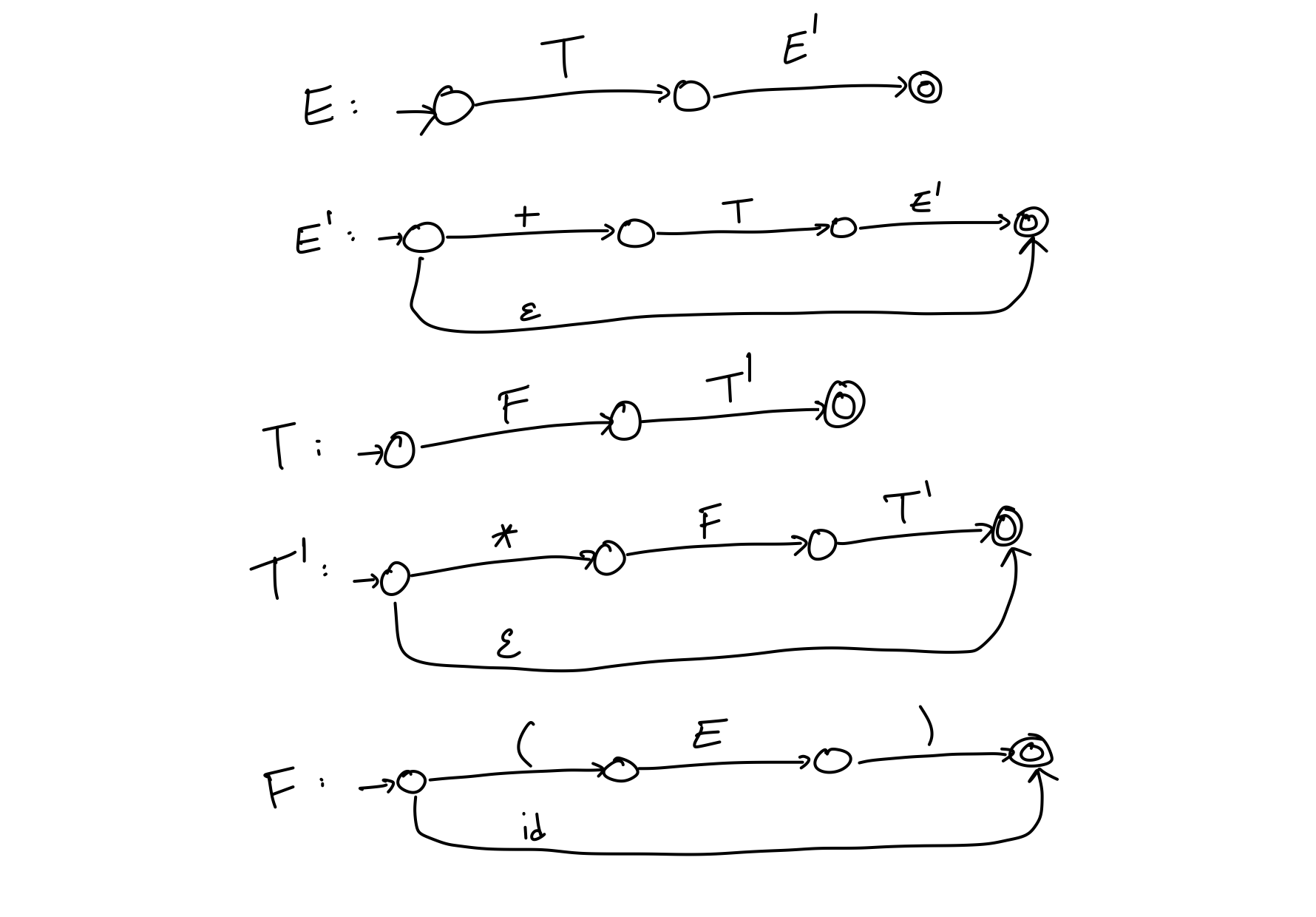
Note that this approach is as powerful as table-driven parsing, only the stack is implicit and hidden; it is the call stack of mutually recursive calls.

Cooperation With Semantic Analyzer: Building Abstract Syntax Trees 🔗

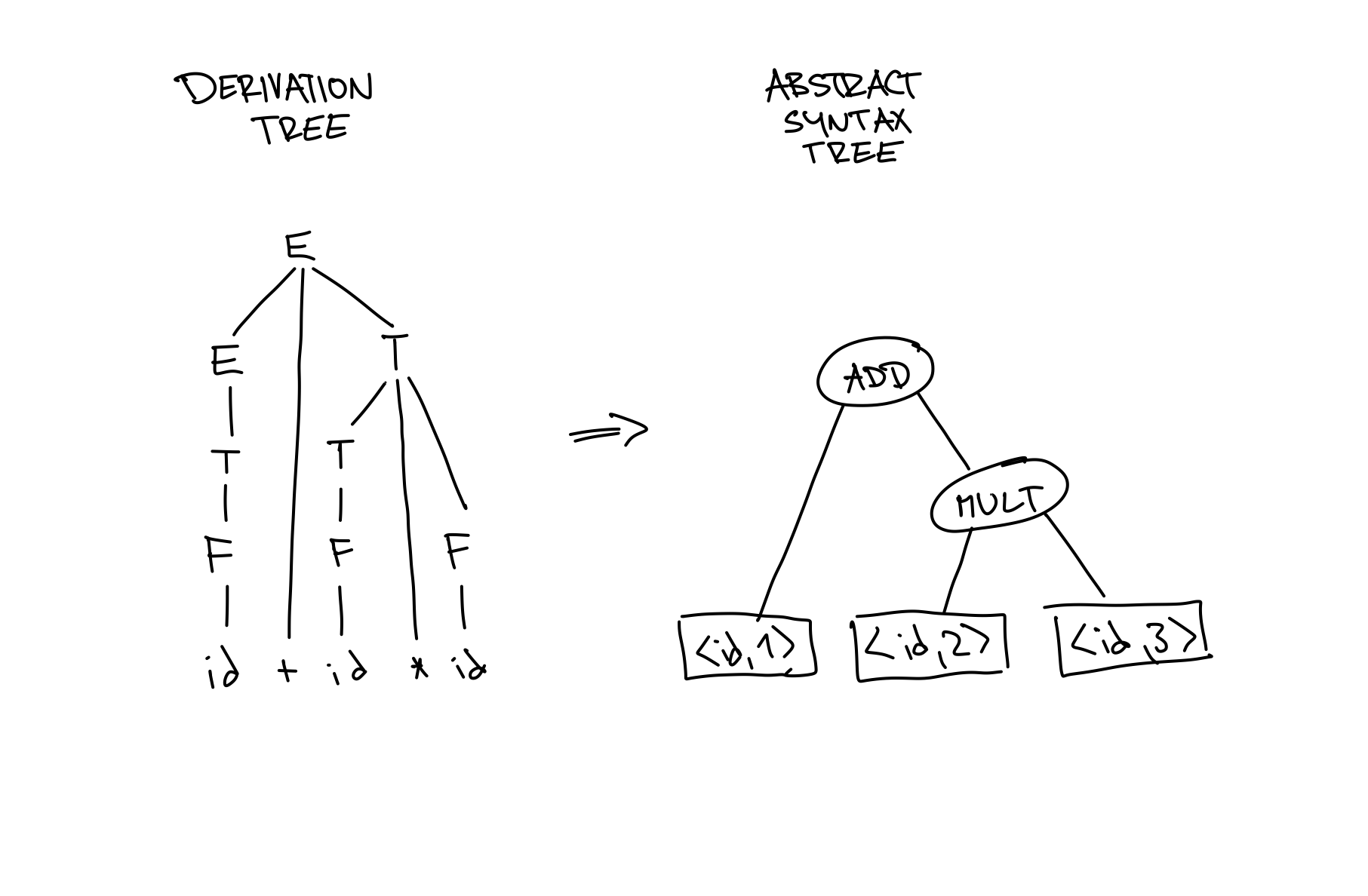
Second objective of the parser is to inform the semantic analyzer about semantically important parts of the program. We could, technically, pass the entire derivation tree to the semantic analyzer, but this is unnecessarily unwieldy. For instance, knowledge of applying production rules in form of E := T does not bring any new information, so we would like to omit such productions while not altering the semantics presented by the derivation tree. On the other hand, productions in the form of E := E + T are semantically important – we’ve recognized an addition operation in the input string. This is done by building an abstract syntax tree (AST) and passing it to the semantic analyzer instead of the derivation tree.

One way to build AST is to extend the original grammar with new terminal symbols related to the AST and to construct a non-deterministic push-down automaton which parses the input while writing the AST to the output in the postfix notation.

Other way is to enrich the symbol (both terminal and non-terminal) instances of the original grammar with attributes and associate production rules with semantic functions. Parser (e.g. recursive descent parser) then parses the input and calls the associated semantic functions, when the given symbol is discovered. The result of the semantic function call is then assigned to the symbol’s attribute.

Non-Deterministic Push-Down Automaton 🔗

ASTs can be easily built by extending the original grammar rules (the ones corresponding to the input program we’re verifying) with new grammar rules for building the AST. For example, the same grammar from previous example can be extended as follows:

P' = {
    E := E + T &ADD  # 1
    E := T           # 2
    T := T * F &MULT # 3
    T := F           # 4
    F := id &ID      # 5
    F := (E)         # 6
}

The only thing we’ve added is three new terminals &ADD, &MULT, and &ID, which belong to the alphabet Δ of AST’s grammar. Now, we’ll use non-deterministic push-down automaton behaving according to these three rules:

1. if a ∈ Σ (input grammar’s terminal) is on top of the stack, then read the input and pop the stack,
2. if A ∈ N (input grammar’s non-terminal) is on top of the stack, then non-deterministically choose the appropriate production rule and expand it in the stack
3. if b ∈ Δ (AST’s terminal) is on top of the stack, then write it to the output.

Rule 3 is the only extension to the classical non-deterministic push-down automaton. Here is how the syntactic analysis of the input id + id * id looks like using NDPA and the grammar G with new extended rules P'. State of the NDPA is denoted as a triplet (input, stack, output), where the top of the stack is on the left.

#  (input       , stack                 , output)
=> (id + id * id, E                     , )
=> (id + id * id, E + T &ADD            , ) # rule 1
=> (id + id * id, T + T &ADD            , ) # rule 2
=> (id + id * id, F + T &ADD            , ) # rule 4
=> (id + id * id, id &ID + T &ADD       , ) # rule 5
=> (+ id * id   , &ID + T &ADD          , ) # pop id from stack
=> (+ id * id   , + T &ADD              , &ID) # write to output
=> (id * id     , T &ADD                , &ID) # pop + from stack
=> (id * id     , T * F &MULT &ADD      , &ID) # rule 3
=> (id * id     , F * F &MULT &ADD      , &ID) # rule 4
=> (id * id     , id &ID * F &MULT &ADD , &ID) # rule 5
=> (* id        , &ID * F &MULT &ADD    , &ID) # pop id from stack
=> (* id        , * F &MULT &ADD        , &ID &ID) # write to output
=> (id          , F &MULT &ADD          , &ID ID) # pop * from stack
=> (id          , id &ID &MULT &ADD     , &ID &ID) # rule 5
=> (            , &ID &MULT &ADD        , &ID &ID) # pop id from stack
=> (            , &MULT &ADD            , &ID &ID &ID) # write to output
=> (            , &ADD                  , &ID &ID &ID &MULT) # write to output
=> (            ,                       , &ID &ID &ID &MULT &ADD) # write to output 

Effectively, we’ve read the string id + id * id and written &ID &ID &ID &MULT &ADD, verifying the syntactic correctnes of the input and transforming infix operators of alphabet Σ into postfix operators of alphabet Δ.

We can also associate a function with each terminal in Δ responsible for building the AST. In our case, we need two types of functions: create_leaf and create_node.

• create_leaf(id_pointer): creates a leaf in the AST pointing to the identifier in the symbol table (which is constructed by the lexer) and returns a pointer to the leaf. This function is associated with &ID.
• create_node(operator, left_operand, right_operand) creates an internal node in the AST, where operator denotes the performed operation (either &MULT or &ADD) and left_operand and right_operand are the pointers to the subtrees on which the operation should be applied.

A push-down automaton will then read the output of the syntactic analysis, &ID &ID &ID &MULT &ADD, call the associated function for each terminal, and push the result to the stack. If the automaton reads &MULT or &ADD, it pops two nodes off the top of the stack and supplies them to the function create_node function, merging the two nodes.

Building ASTs With Attributes and Semantic Functions 🔗

In fact, the derivation tree does not have to be build explicitly at all. Instead, we can have semantic functions associated with each production rule and attributes associated with each symbol instance. Semantic functions will be responsible for incrementally building the AST tree while attributes in the derivation tree will hold pointers to the corresponding “dual” AST subtree.

In our example, each symbol will have a single attribute nptr (node pointer), which can be accessed via the dot notation, e.g. E.nptr. Semantic functions then access and assign to those attributes. We will use the function create_leaf and create_node as defined above. The production rules P can be extended as follows:

P'' = {
    E := E' + T {E.nptr = create_node(&ADD, E'.nptr, T.nptr)}
    E := T      {E.nptr = T.nptr}
    T := T' * F {T.nptr = create_node(&MULT, T'.nptr, F.nptr)}
    T := F      {T.nptr = F.nptr}
    F := id     {F.nptr = create_leaf(id)}
    F := (E)    {F.nptr = E.nptr}
}

Note that E and E' are different instances of the same non-terminal.

Effectively, for every semantically important production, we have some semantic function which creates some (leaf or internal) node and assigns the pointer to it to an attribute. If the production is not semantically important, the pointer is just passed from the child to the parent up the tree. Parser can now parser the input and just call the semantic functions and it will build the corresponding AST.